声明：本文参考课程《轻松学统计》，授课教师：罗良清。

1 统计的含义

统计工作
政府统计和民间咨询机构所从事的工作。是搜集数据、整理数据、分析数据等组成的系列工作的总称。
统计资料
统计工作所得到的资料。如《2015年中国统计年鉴》
统计学
研究如何进行数据搜集、整理、分析的一门学科。通过对现象、所研究的事物或对我们所发现的问题的数据搜集、整理、分析来发现它内部的发展规律，并进行预测。

2 统计学的应用领域

只要有数据，就有统计学。经济统计、管理统计、生物统计、物理统计、医学统计、气象统计、心里统计、教育统计…人们可以通过统计来认识社会、认识事物的本质。

3 统计学的研究方法

大量观察法
时间拉长、范围放大
统计指标法
统计分组法
将杂乱无章的数据系统化、条理化的过程。能反映总体的内部结构和一般的发展水平和规律。
归纳推理法
通过部分信息推导出全部总体的信息。

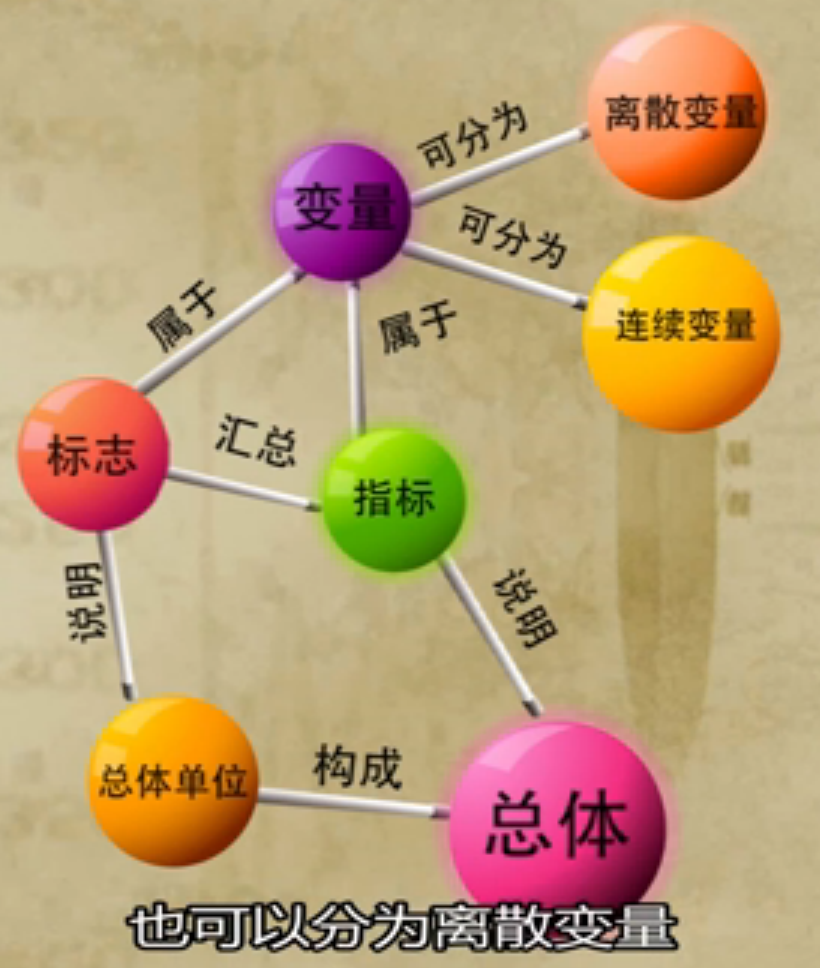
4 基本概念

总体

由许多性质相同的总体单位所组成的整体。（相当于集合，由许多性质相同的元素所组成的整体。）

特点：大量性、同质性（总体单位在某些标志表现上）、差异性（总体单位在大部分标志表现上）
分类：有限总体（总体单位数是有限的）、无限总体（总体单位数是无限的）
注意：总体有单位，与研究目的联系在一起。比如，中国不是一个总体，中国的人口是总体，每个居民是总体单位

总体单位

组成总体的每一个事物。简称个体。

标志

反映总体单位特征的名称。

品质标志：说明属性特征的名称，不能用数值表示。（quality）
数量标志：说明数量特征的名称，可以用数值表示。（quantity）
标志的表现就是标志具体的属性或数值。

举个栗子

要调查某大学学生的四六级考试情况，总体：该大学本学期参加四六级考试的所有学生；总体单位：每个学生；标志：姓名（品质标志）、性别（品质标志）、民族（品质标志）、身高（数量标志）、体重（数量标志）、年龄（数量标志）、三围（数量标志）。。。

指标

说明总体数量特征的名称和数值。如人均GDP为5.2万元
分类：

绝对指标、相对指标、平均指标；
数量指标（反映总体广度的指标）、质量指标（反映总体深度的指标）。

标志与指标的区别与联系

指标是说明总体特征的，标志是说明总体单位特征的；
指标反映数量特征；标志反映品质和数量特征。
指标值往往由数量标志值汇总而来；
在一定条件下，数量标志和指标存在着变换关系。

变异

所有的变动。指标会变，标志也会变。

变量

可变的标志及指标。
分类：

连续变量（取值是连续的，可以带小数（如年龄））、离散变量（取值是间断的，只能为整数）
定类（如人可分为男、女两类）、定序（如一级、二级、三级产品）、定距（如温度分华氏、摄氏）、定必变量（可进行四则运算如GDP）。

5 统计调查

统计资料的搜集过程。

搜集的资料

原始资料：统计调查过程中直接搜集到的资料，其信息量多于次级资料。
次级资料：由他人搜集、分组、整理、再分析的现成资料（又：第二手资料）。通常可在公报、年鉴和网站获得。

基本要求

全面
及时
准确（首先要保证的）

方法

直接观察法
采访法
电话访问
邮寄调查
网络调查
卫星遥感

方案设计

确定调查目的（Why）
确定调查对象（Whom）：调查单位
明确调查内容和调查表（What）
确定调查时间（When）：调查的起止时间，调查资料所属的时间
组织方式的实施

误差

可消除误差

登记误差
系统性误差

不可消除误差

抽样误差：样本与总体总是有差别的！抽样误差可控并可以计算。
度量衡误差：如，用尺测量长度，尺子带来的测量误差就属于度量衡误差，可通过多次测量求平均的方式减小该误差。

《轻松学统计》课程笔记（一）：统计与统计调查