描述性统计
统计学的大分类
- 描述统计学
使用特定的数字或图表来体现数据的集中和离散程度。如:平均值,最值,值的分布。 - 推断统计学
根据样本数据推断总体数据特征。如:产品质量检查时使用抽检。
集中趋势
一组数据向中心值靠拢的程度。
- 均值:描述平均水平。
- 中位数:描述中等水平。
- 众数:描述一般水平。
| 优点 | 缺点 | |
|---|---|---|
| 均值 | 充分利用所有数据,适用性强 | 容易受到极端值影响 |
| 中位数 | 不受极端值影响 | 缺乏敏感性 |
| 众数 | 当数据具有明显的集中趋势时,代表性好;不受极端值影响 | 缺乏唯一性:可能有一个,或多个,或没有 |
离散程度的描述
一组数据,距离中心越远,即极差或方差或标准差越大,则越离散。
- 极差:最大值-最小值
- 方差:每个数据距离中心的距离的平方的均值。其单位是原数据单位的平方。
- 总体方差:$$\sigma^{2}=\frac{1}{N}\sum\limits_{i=1}^{N}(X_i-\mu)^2$$
- 样本方差:$$\sigma^{2}=\frac{1}{n-1}\sum\limits_{i=1}^{n}(x_i-\bar x)^2$$
- 标准差:方差的算术平方根。其单位与原数据单位一致。
- 总体标准差:$$\sigma=\sqrt{\frac{1}{N}\sum\limits_{i=1}^{N}{(X_i-\mu)}^2}$$
- 样本标准差:$$\sigma=\sqrt{\frac{1}{n-1}\sum\limits_{i=1}^{n-1}{(x_i-\bar x)}^2}$$
其中,$X_i$表示总体中第i个数据的值,$x_i$表示样本中第i个数据的值;$\mu$表示总体数据集的均值,$\bar x$表示样本数据集的均值。
常见统计图表
直方图
- 频数直方图
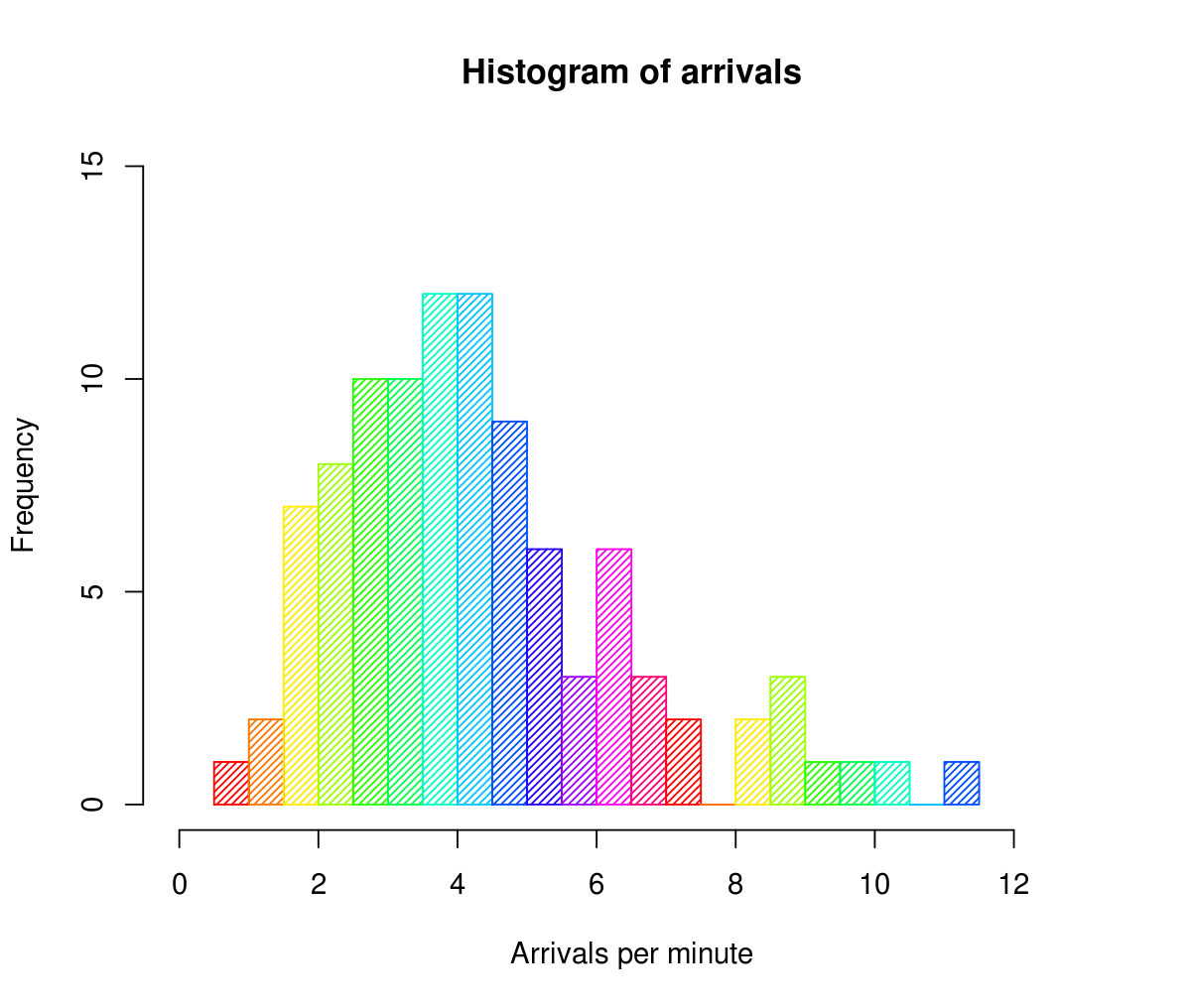
- 频率直方图
柱形图
显示一段时间内的数据变化或显示各项之间的比较情况。
柱形图与直方图的区别:
- 横坐标不同。直方图的横坐标是同一个变量的分组划分,而柱形图则是不同的组别。
- 作用不同。直方图用于显示一组数据的分布情况,柱形图则是用于比较不同组别的数据差异。
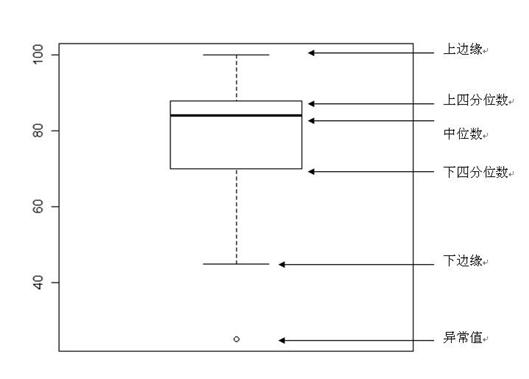
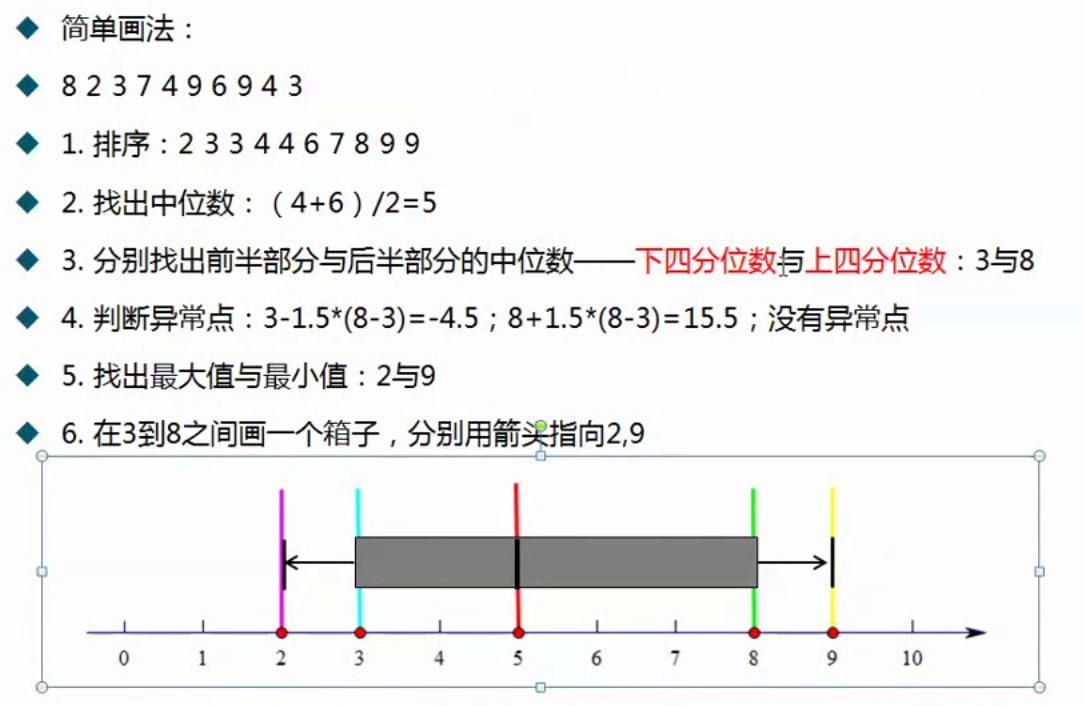
箱线图
- 下四分位数:Q1,将所有数据从小到大排列,排在第25%的位置的值。
- 上四分位数:Q3,将所有数据从小到大排列,排在第75%的位置的值。
分位数的位置:选择四分位的百分比值y,即样本总量n,分位数的位置可如下计算:
$$L_y = n * \frac{y}{100}$$- 情况1:若L是整数,则取L和L+1的平均值;
- 情况2:若L不是整数,则取下一个最近的整数。
如:对于2,3,4,5,6这组样本数据,下四分位数的$y=25$,所以$L = n * \frac{25}{100} = 5 * 0.25 = 1.25$,故下四分位数应取位于第2位(L=2)的3.
- 四分位距:IQR,为Q3-Q1。
- 异常点:小于Q1-1.5IQR,或大于Q3+1.5IQR。
- 上边缘:除异常点以外的数据中的最大值。
- 下边缘:除异常点以外的数据中的最小值。
茎叶图
茎叶图可以在保留全部数据信息的同时,直观地显示出数据的分布情况。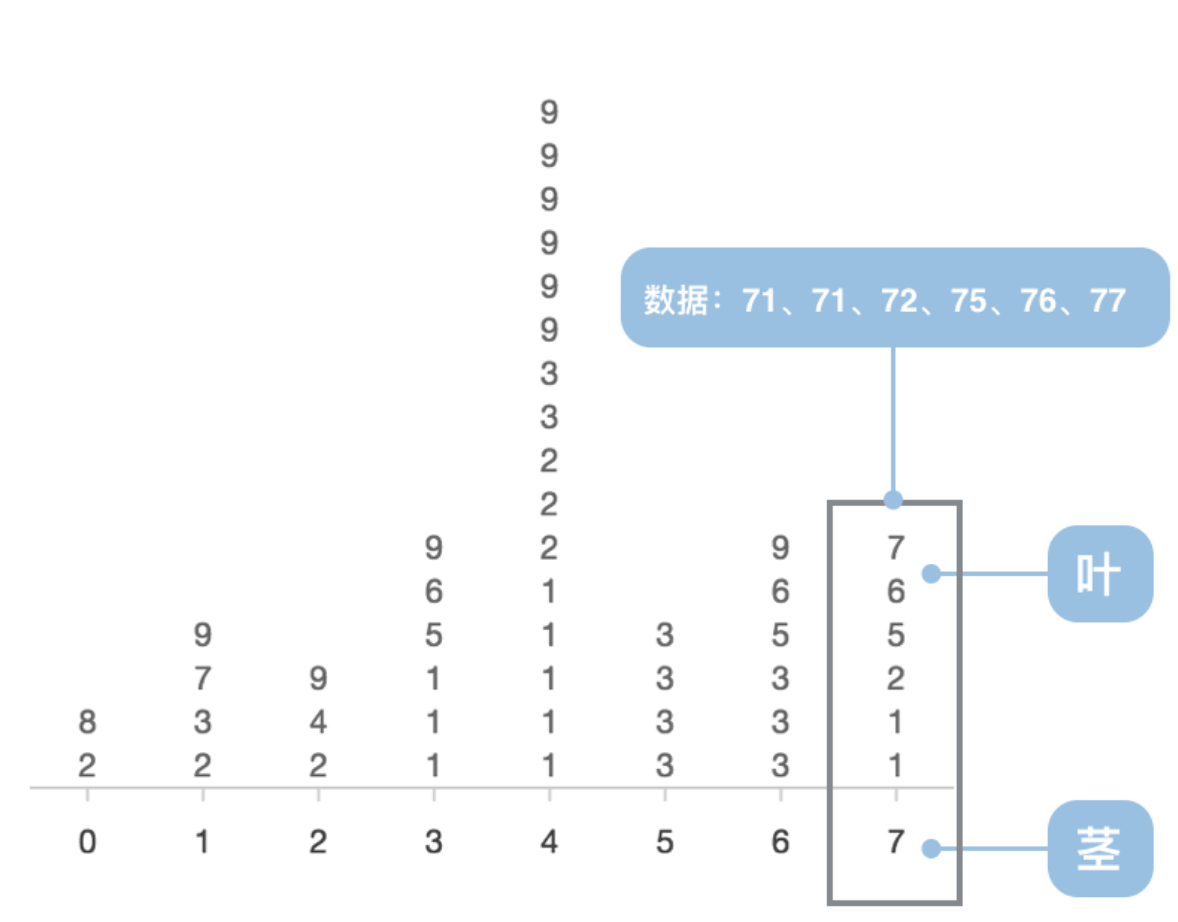

线图
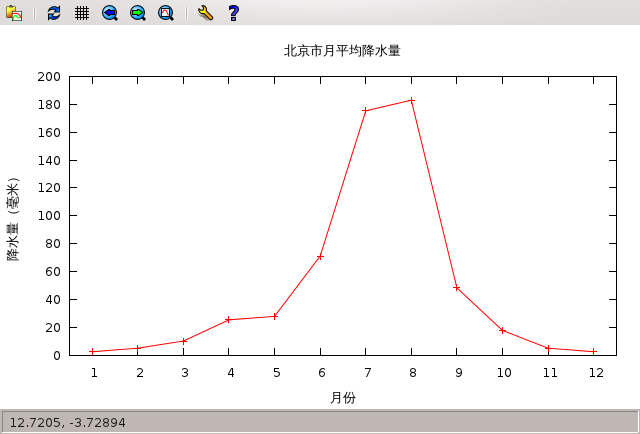
饼图
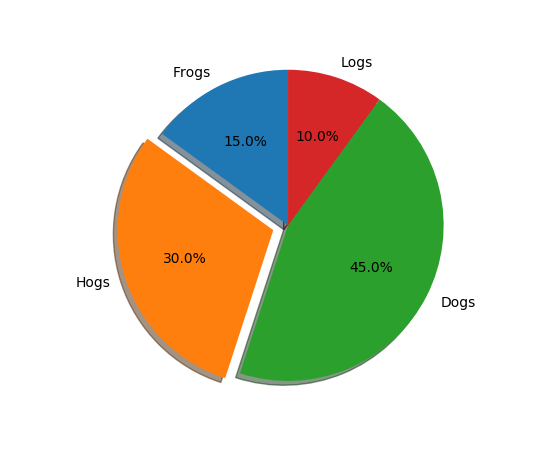
古典概型与几何概型
试验
对某种自然现象做一次观察或进行一次科学试验。
随机试验的特征
- 可以在相同的条件下重复进行。
- 试验的可能结果不止一个,但在试验前可以知道所有可能的结果。
- 试验前不确定哪个结果会出现
样本空间
对于随机试验E,E的所有可能结果组成的集合称为E的样本空间,记为S。
- 例1:抛掷一枚骰子,观察出现的点数。$S = \lbrace1,2,3,4,5,6\rbrace$
- 例2:记录某车站某日某时刻的等车人数。$S = \lbrace0,1,2,3,…\rbrace$
- 例3:考察某地区12月的平均气温。$S = \lbrace t|T_1<t<T_2\rbrace$
样本点
样本空间S中的元素,即E的每个可能的结果,称为样本点。
随机事件
试验E的样本空间S的某个子集,称为E的随机事件,简称事件。一般用大写字母A、B、C…表示。
如:在抛骰子试验中,“所得点数为偶数”是一个随机事件A,“所得点数为1”是一个随机事件B。
基本事件
由一个样本点组成的单点集。
如:在抛骰子试验中,“所得点数为1”是一个基本事件B。该实验共有6个基本事件。
必然事件与不可能事件
- 事件发生:在每次试验中,当事件中的某个样本点出现时,称为事件发生。
- 必然事件:在每个试验中一定会发生的事件。在抛骰子试验中,事件C”点数小于等于6点”是必然事件。
- 不可能事件:在每个试验中一定不会发生的事件,用$\varnothing$表示。在抛骰子试验中,事件D”点数大于6点”是不可能事件。
事件关系
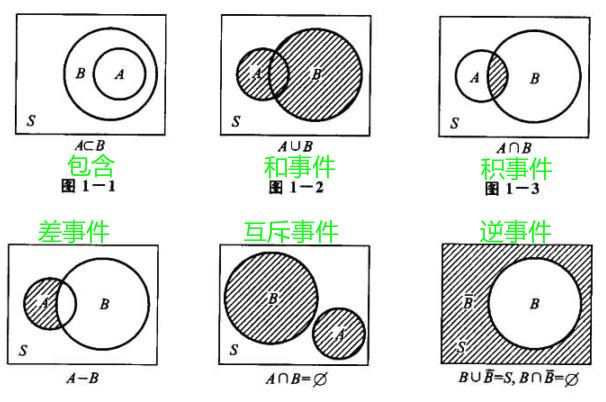
事件运算定律
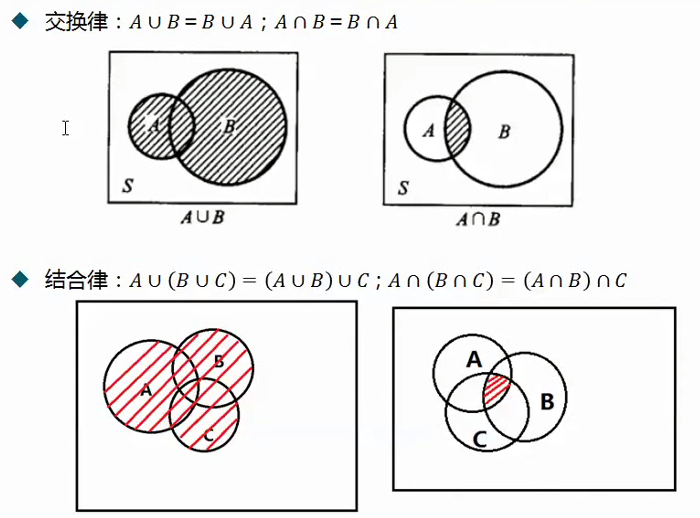
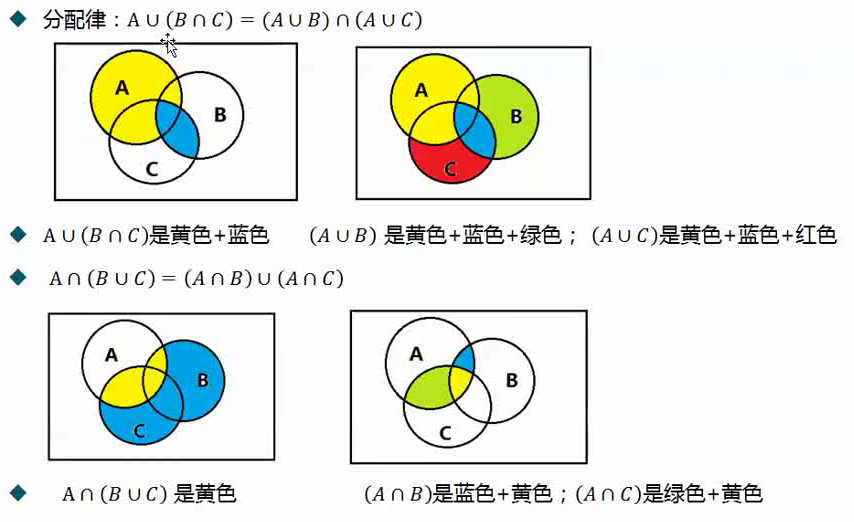
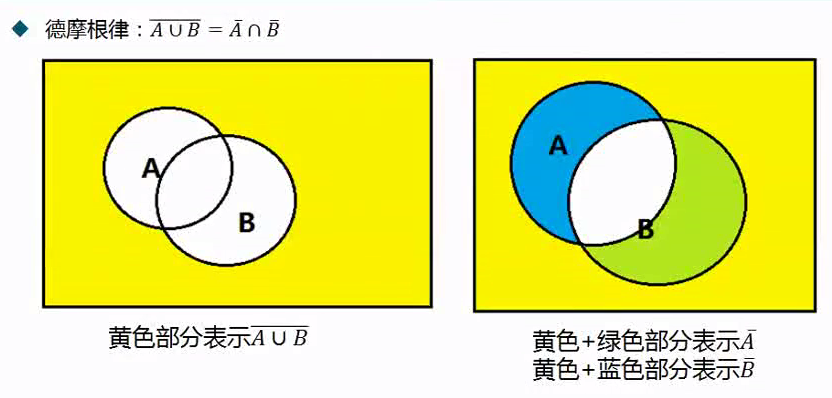
概率
在相同条件下,重复n次试验,事件A发生的
- 频数:A发生的次数$n_{_A}$
- 频率:$\frac{n_{_A}}{n}$
- 概率:大量试验证明,当试验的重复次数n逐渐增大时,事件A发生的频率会逐渐稳定于某个常数p。这个p就是事件A发生的频率,用于表示在一次试验中,事件A发生的可能性大小。记为P(A)。
概率的需要满足的条件
- 非负性:$0 \leqslant P(A)\leqslant 1$
- 规范性:对于必然事件S,有P(A)=1
- 可列可加性:对于互斥(两两不相容)事件$A_1$,$A_2$,$A_3$…,即$A_i \cap A_j= \varnothing (i \neq j)$,有$$P(A_1\cup A_2 \cup …) = P(A_1)+P(A_2)+… $$
概率的性质
- 不可能事件发生的概率为0,即$$P(\varnothing)=0$$
- 有限可加性:对于互斥(两两不相容)事件$A_1$,$A_2$,$A_3$…$A_n$,即$A_i \cap A_j= \varnothing (i \neq j)$,有$$P(A_1 \cup A_2 \cup …A_n) = P(A_1)+P(A_2)+…P(A_n) $$
- 对于A,B两个事件,若$A \supset B$,则$$P(A-B)=P(A)-P(B); P(A) \geq P(B)$$
- 对于任一事件A,有$$P(A) \leqslant 1$$
- 对于任一事件A,有$$P(\bar A)=1- P(A)$$
- 加法公式:对于A,B两个事件,有$$P(A \cup B)=P(A)+P(B)-P(AB)$$ 推广:$$P(A_1 \cup A_2 \cup A_3)=P(A_1)+P(A_2)+P(A_3)-P(A_1A_2)-P(A_1A_3)-P(A_2A_3)+P(A_1A_2A_3)$$
古典概型
- 有限性:试验的样本空间包含有限个元素。
- 等可能性:试验中每个基本事件发生的概率相等。
满足有限性和等可能性的试验称为古典概型。
几何概型
- 无限性:试验的样本空间包含无限个元素。
- 等可能性:试验中每个基本事件发生的概率相等。
满足无限性和等可能性的试验称为几何概型。
$ P(A)=\frac{构成事件A的区域长度(面积或体积)}{实验的全部结果所构成的区域长度(面积或体积)}$
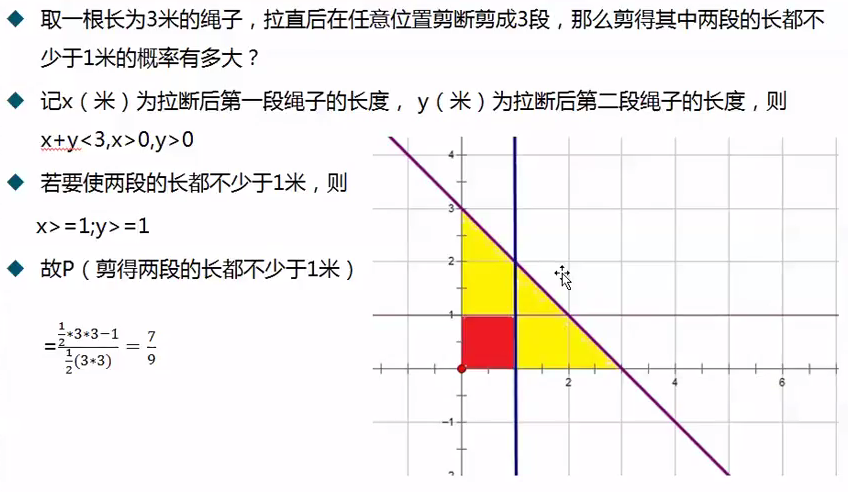
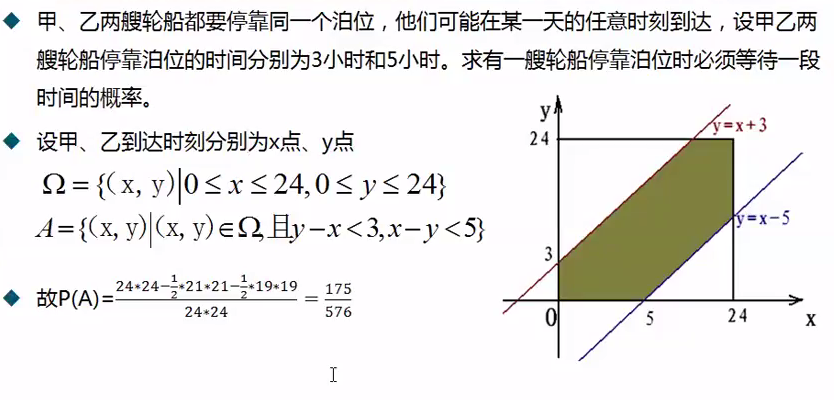
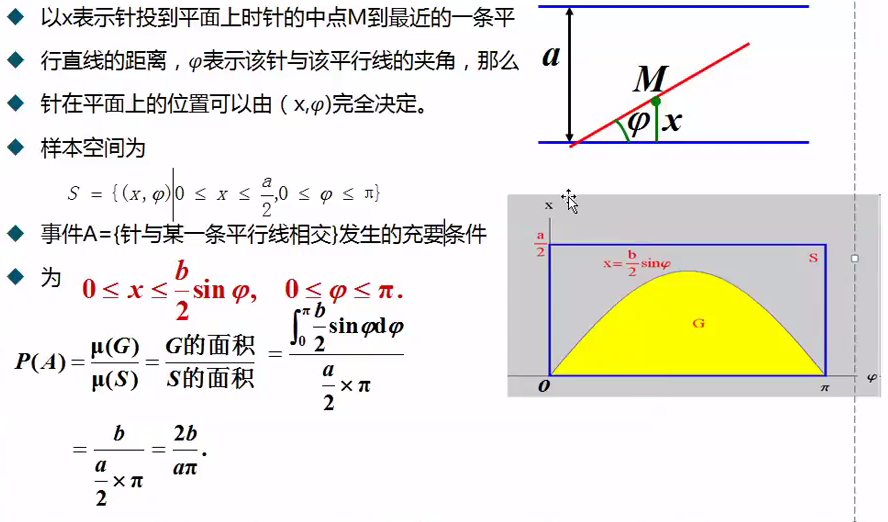
Buffon投针试验
18世纪,Buffon提出以下问题:假设有一个以平行且等距(间距为a)木纹铺成的地板,现随意抛一支长度为b的针(b小于a),求针和其中一条木纹相交的概率。